TOUCH THE SECURITY Powered by Security Service G

単一換字式暗号(たんいつかえじしきあんごう、Simple substitution cipher)とは、換字式暗号の一種で、平文の文字に対して、暗号文の文字が常に同じ文字に変換されるような暗号のこと。(引用:フリー百科事典『ウィキペディア(Wikipedia)』(単一換字式暗号 より)
単一換字式暗号で広く知られているのは「シーザー暗号」と呼ばれるもので、暗号アルゴリズムも単純なため、紙とペンという古典的な道具だけでも一定の労力と時間で、解読することが可能な暗号文です。
今回は、単一換字式暗号についての仕組みや解読法などをご紹介します。
単一換字式暗号について
単一換字式暗号は、平文の文字に対して、必ず同じ暗号文の文字に変換される暗号のことです。換字式暗号(平文を1文字から数文字単位で異なる文字などに変換して暗号文を作る暗号)の中では、単純なアルゴリズムの暗号です。
例えば、平文の「a」が、暗号文の「c」に ”必ず” 暗号化されるのであれば、それは単一換字式暗号です。
上述でも紹介したシーザー暗号は、暗号化アルゴリズムが単純であり、使用される文字の種類の数しか鍵空間を確保できないことが強度の面で大きな問題点となってしまいます。
主流であったシーザー暗号が時代が進むにつれ安全ではなくなり、もう少し複雑な暗号が使われるようになります。その暗号が、単純なシーザー暗号よりもはるかに大きな鍵空間を確保できる、変換リストを利用した単一換字暗号です。
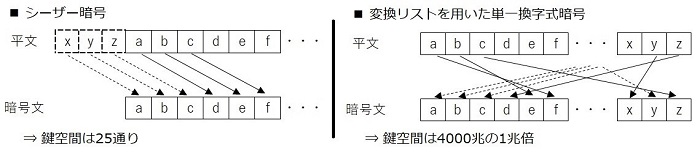
単一換字暗号であれば、英語アルファベット26文字のみが対象だとしても26×25×24×23×22…3×2×1 = 4000兆の1兆倍もの鍵空間を確保できることになります。これは、シーザー暗号の鍵空間とは比較にならない大きさです。
これだけの鍵空間を確保できると、解読方法の実行は現実的ではなく、シーザー暗号よりもより解読が困難になったことがわかります。
単一換字式暗号について
シーザー暗号とは、単一換字式暗号のなかでも最も有名な暗号として知られており、それぞれの文字を特定のルールに沿ってアルファベット順で決まった数だけずらしていくことで解読する暗号手法です。
古代ローマで活躍したガイウス・ユリウス・カエサル(シーザー)も暗号を使っていたことが知られています。後の歴史家スエトニウスは書物「皇帝伝」に、カエサルは各文字をそれぞれ同じ文字数だけシフトして暗号を作成したと記しており、この暗号は「シーザー暗号」と呼ばれています。
たとえば、それぞれの文字を「3つ」づつずらすというルールの場合、平文の「a」→ 暗号文の「d」、「b」→「e」、「c」→「f」という具合に暗号化されていきます。「x」「y」「z」のように3つシフトすると「z」を超えてしまう場合は、次の文字は再び「a」に戻るというルールでシフトされ、それぞれ「a」「b」「c」と暗号化されました。平文が “hello” の場合、暗号文は “khoor” になるわけです。
現代の暗号学では換字式暗号の一種である単一換字式暗号(単換字式暗号)に分類されます。
シーザー暗号について詳しく知りたい方は、こちらの記事も参考にしてください。
Pythonを用いて単一換字式暗号を暗号化してみる
実際に変換リストを用いた単一換字式暗号を行うプログラムを「Python」で実装してみました。暗号化を行い、結果を確認してみましょう。
解析作業を行うなどの便宜上、平文を英語小文字、暗号文を大文字で表現しています(入力値のエラーチェックなどは省略。
♦ソースコード
# plain_char_list > 平文の文字リスト
# subst_char_list > 換字リスト
# plain_text > 暗号化対象の平文
def SubstituteCipher(plain_char_list, subst_char_list, plain_text):
cryptogramList = []
for char in plain_text:
if char in plain_char_list:
index = plain_char_list.index(char)
cryptogramList.append(subst_char_list[index])
print('平 文: ' + plain_text)
print('暗号文: ' + ''.join(cryptogramList))
if __name__ == '__main__':
plain_char_list = 'abcdefghijklmnopqrstuvwxyz'
subst_char_list = 'ZYXWVUTSRQPONMLKJIHGFEDCBA'
SubstituteCipher(plain_char_list, subst_char_list, ‘ilovemotorcycles’)
♦実行結果
平 文: ilovemotorcycles
暗号文: ROLEVNLGLIXBXOVH
「ilovemotorcycles」が「ROLEVNLGLIXBXOVH」に暗号化されました。
平文の「i」が9文字分シフトされ、暗号文の「R」に暗号化されています。もしもこれが「シーザー暗号」であれば、平文の「c」「e」はそれぞれ「L」「N」に暗号化されるはずですが、上記の「変換リスト」を用いた「単一換字式暗号」では、それぞれ「X」「V」に暗号化されていることが確認できます。
上記は比較的単純な暗号でしたが、より複雑な単一換字式暗号の解読には「頻度分析」と呼ばれる手法が有効です。
頻度分析とは?
頻度分析とは、頻度分析(Frequency analysis、ひんどぶんせき)は、平文と暗号文に使用される文字や文字列の出現頻度を手掛りとして利用する暗号解読法のことである。平文の言語の統計的特徴を前提とし、暗号文のみを使用して解読を行うため、暗号文単独攻撃に分類される。(引用:フリー百科事典『ウィキペディア(Wikipedia)』頻度分析)
文字がどのくらい頻出しているかの傾向を分析し、それを手がかりとして暗号解読を行うのが頻度分析です。
次は、実際に頻度分析を用いて、暗号を解読してみましょう。
単一換字暗号を頻度分析を踏まえた上で解読してみる
例として作成した単一換字暗号を、頻度分析の概要を踏まえた上で解読してみましょう。
まず、英文素材から選んだある英文を、スペースを削除したうえですべて小文字に加工した文字列を前項のプログラムで暗号化したところ、以下の暗号文に暗号化されました。
つぎに、変換リストを用いずにこの暗号文を解読する方法について考えてみましょう。暗号文が少し長いので、一見すると解読が困難に感じるかもしれませんが、むしろ暗号文が長いほど解読は有利になります。
暗号鍵となる変換リストを総当たりで試すのは、膨大な鍵空間を試さなければならなくなるので現実的ではありません。
しかし、いくら鍵空間が大きくても、単一換字式暗号は「平文のそれぞれの文字が、暗号文のどの文字に暗号化されるか」が決まってしまっているという大きな弱点を抱えています。そこで、「頻度分析」の解読手法が有効になってきます。
英文を例に考えてみます。
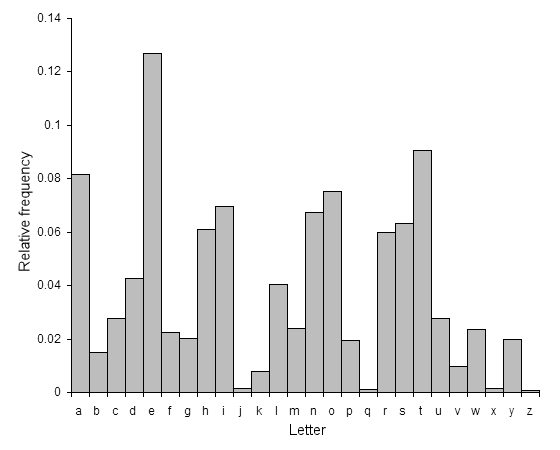
英語文における文字の使用頻度分布 via Wikipedia Commons
上記の分布のように、一般的に使用される頻度の高い文字や、文字の組み合わせの統計がデータとして存在します。
これらを見ると、1文字単体としてみた場合、最も使用される文字は「e」であり、次に使用される文字は「t」、以下「a」「o」「i」「n」「h」と続きます。逆に使用頻度が低い文字として「z」「q」「x」「j」が挙げられます。
また、2文字、3文字といった組み合わせの場合も、出現頻度の高い文字の組み合わせが存在します。3文字の場合「t-h-e」「i-n-g」「a-n-d」「i-o-n」の組み合わせの出現頻度が高く、2文字の場合は「t-h」「h-e」「o-o」の文字の組み合わせが高い頻度で出現します。
まとめ
これまでの話のまとめは、下記になります。
- 鍵空間が大きくても、暗号化アルゴリズムに脆弱性がある暗号は安全ではありません。
- 単一換字式暗号は、どの文字がどの文字に暗号化されるか決まっている弱点を抱えています。
- そういった弱点により、単一換字式暗号は頻度分析を利用した解読方法が有効です。
- 暗号解読方法には、暗号鍵の総当たり攻撃のほかにも、頻度分析と呼ばれる方法が存在します。
- 暗号文は長ければ長いほど、解読には有利です。
また、時代が中世に進むと、頻度分析を用いた解読法により、変換リストを用いた単一換字式暗号も安全ではなくなります。それにより、「多表式」の変換リストに加えて暗号鍵の文字列を用いる「ヴィジュネル暗号」や、単一換字式暗号の弱点を克服するために、平文の同じ文字が出現個所によって異なる文字に暗号化する「換字式暗号」も開発されていきます。
そして、時代とともに換字式暗号も解読が進み、近代になると「エニグマ」に代表されるような「機械式」の換字式暗号や、プログラム可能な電子計算機による「電子暗号」の時代に突入しています。
-
参考文献
- 暗号技術入門 第3版 秘密の国のアリス 結城浩著 SBCreative
- みんなのPython【第4版】柴田淳著 SBCreative


