TOUCH THE SECURITY Powered by Security Service G

コンピューター科学の巨人、アラン・チューリング。彼が考案したチューリングマシンは、コンピューターの原理となり、その後、コンピューター実機の開発が始まっていきます。
しかし、チューリングは最初からコンピューターの原理を考案しようとしたわけではありませんでした。チューリングマシンからコンピューターが生まれるまでには長い物語があります。
今回は、チューリングを主人公に描かれた映画「イミテーション・ゲーム」をもとに、チューリングマシンについて見ていきましょう。
目次
映画「イミテーション・ゲーム」から読み解くチューリングとその功績
コンピューターの原理を作ったイギリスの数学者アラン・チューリング(1912〜1954)を主人公にした映画「イミテーション・ゲーム」は、数学の巨人アラン・チューリングが、ヒトラーの最強暗号「エニグマ」の解読に挑み、間接的に多くの人の命を救った英雄物語です。
映画の内容は、チューリングの光の部分だけでなく、陰にも触れています。チューリングは幼い頃からゲイであり、女性に恋心を抱くことができませんでした。しかし、当時のイギリスは、同性愛が犯罪だったとされている時代です。彼は、とある事件に巻き込まれたとき、自身の同性愛である点に悩み、最後は悲劇的な結末を迎えます。
ただチューリングは、生涯で一度だけ、エニグマ解読の拠点ブレッチリーパークで同僚だった女性数学者ジョーン・クラークに恋をして、婚約をしています。しかし、それは恋心だったのか、それとも同僚数学者に対する敬意だったのか。その辺りも、映画では美しくも切なく描き出されています。

イミテーション・ゲーム/エニグマと天才数学者の秘密
英政府が50年以上封印した、暗号解読の裏に隠された秘密とは?
ベネディクト・カンバーバッチが挑む、<天才数学者>の驚愕と感動の実話。
チューリングマシンとは
チューリングマシン(チューリング機械)とは、1936年にアラン・チューリングが発表した論文の中で「計算する」ことを定義した仮想的な計算機です。構造は単純で、この計算機で計算をして、機械がデータを出力できるならば計算できる、データの出力が不可能ならば計算できないと定義されています。
この計算機は、コンピューターの仕組みの原理・基礎をついていて、チューリングマシンについて深く知ることで、現在あるコンピューターの能力を理解できるほどです。
計算機は、一本のテープ、そしてそれを読み取るヘッドが1つあるだけです。この計算機でできることは、テープに文字を書くこと、ヘッドを右および左に1文字分のみ移動すること、文字を読み取ることのみです。これは、このマシンで計算の手順を書き込むことができること、そしてその計算が可能であることを示しました。
チューリングはコンピューターの原理を発明したのか
チューリングマシンの概念は、現代のコンピューターと極めてよく似た構造で、ここから「チューリングはコンピューターの原理を発明した」と言われます。確かに、コンピューター科学の教科書を開くと、最初にそろばんや石盤の話が出て、次にパスカルの機械式計算機、そしてチャールズ・バベッジの差分機関、階差機関が登場し、それからチューリングマシンが登場して、コンピューターの近代史が始まるかのように解説をされていることが多くあります。
しかしチューリングは、コンピューターを作るための目的でこの計算機を作ったわけではありません。チューリングが論文を発表した数十年も前、当時多くの数学者に影響を与えた数学者ダフィット・ヒルベルト(1862〜1943)という人物が、数学というシステムを整えるために「そこにある数学が絶対に間違わない、ということを数学で証明する」運動をはじめました。これはヒルベルト・プログラムと呼ばれます。このプログラムの目的は、数学の命題を正しい論理式(定理か否か)としてあらわす、数学的に論証できるアルゴリズムを開発することでした。
これを「決定問題」といいますが、チューリングはこの「決定問題」を解決するために、チューリングマシンを開発しました。
チューリングは純粋な数学的な難題を解決する手段にチューリングマシンを用いました。結果、それがコンピューターの原理になっていることに後で気がつき、15年後に自身でもACE(エース)と呼ばれるコンピューターの開発を行っています。

By Antoine Taveneaux (Own work) [CC BY-SA 3.0], via Wikimedia Commons
ACEコンピューターはチューリングマシンの論理モデルを具現化したもの。
写真はプロトタイプモデルの「PILOT ACE」。
数学の危機 ~ゲーデルの唱えた不完全性定理~
数学の危機とは、1930年、ハンガリーの数学者クルト・ゲーデルが証明した不完全性定理のことです。これは世界の数学者にとって衝撃的なできごとでした。
それまで数学は、完全な学問だと思われており、世の中のすべての現象は、数学で記述ができると考えられていたのです。優秀な者が世界を数学で記述してしまえば、この世界は人類の思い通りになると信じられていました。
この時代に、クルト・ゲーデルによって「数学は不完全であり、世界のすべてを記述できるなどということはあり得ない」という不完全性定理が提唱されます。ゲーデルは、数学は思ったよりも無力であるということを示しました。しかしゲーデルの説は、論理学という数学の一分野からの見地であったため、数学の万能性を依然信じ続ける学者も多くいました。
「数学者はいち早く現実を受け入れ、それを前提に新しい数学を構築していく必要がある」 そう考えたチューリングは、代数学の世界でも数学の不完全性を証明しようと考えます。
チューリングによる不完全性定理の証明 ~チューリングマシン~
ゲーデルが唱えた不完全性定理の証明にあたり、チューリングは、数式の駆使といった従来の発想を超え、「チューリングマシン」を用いた論理モデルでの証明を試みます。
チューリングマシンはどんな計算でもできるマシンです。しかし、チューリングマシンに計算できない問題があると証明されれば、この世の中に計算できない問題が存在することになります。
このような仮説のもと、チューリングは代数学的に数学の不完全性を証明しようとしました。前提となる「どんな計算でもできるマシン(チューリングマシン)」を定義するにあたり、チューリングがまず行ったことは、私たちが行っている「計算」を”要素”に分解することでした。
例えば、「1+2=3」という計算の場合、要素として分解するとまず「1という数字を記憶する」「+記号を見て、演算の種類を記憶する」「2という数字を記憶する」「=記号を見て、記憶した数字を記憶した種類の演算をする」「演算結果を記録する」ということを組み合わせて行っています。
この工程をさらに分割できない要素にまで分解していった結果として、「紙テープ」「0と1を書き込むことができるヘッド」を備える、仮想機械チューリングマシンの概念を定義しました。あとは「0を書き込んで右に1コマ移動」「紙テープの文字を読んで、左に1コマ戻る」などの命令を並べたプログラムさえ書ければ、計算の要素機能をすべて備えているチューリングマシンは、どのような計算でもこなせるはずです。
ですが、次はこの「何でも計算できるはずのマシン」に「計算できない問題が存在する」という、矛盾を証明する必要がありました。
矛盾の証明 ~カントールの対角線論法~
矛盾をどうやって証明すれば良いのかと考えたチューリングは、19世紀のドイツの数学者カントールが行った、数学の証明方法を参考にしました。
カントールが挑んだのは、「自然数と実数はどちらが多いか」という問題です。自然数というのは1、2、3…という普通の数のことで、実数というのは3.16や7.635などの小数や分数なども含む数のことで、誰がどう見ても、実数の方が個数は多いと思うでしょう。1と2の間だけで考えると、自然数は1と2の2個しかないのに、実数の方は2.05、2,52432といくらでも作ることができるため、実感としては、実数の方が多く感じます。
カントールは「実数の方が多い」ということをきちんと証明しようとして、ユニークなロジックを使いました。
まず、「自然数と実数の個数は同じ」という前提条件を立て、これの矛盾点を探す方法です。矛盾が見つかれば、「個数は同じではない」ということが証明できます。カントールはまず0と1の間の実数を無限に並べた表を作り、それに1から順に背番号をつけていきました。この表は、右方向にも下方向にも無限に続きます。無限に続くのだから、すべての実数が列挙され、それに背番号がつけられているので、同じ数だけの自然数があることになります。実数の個数と自然数(背番号)の個数は同じになっています。
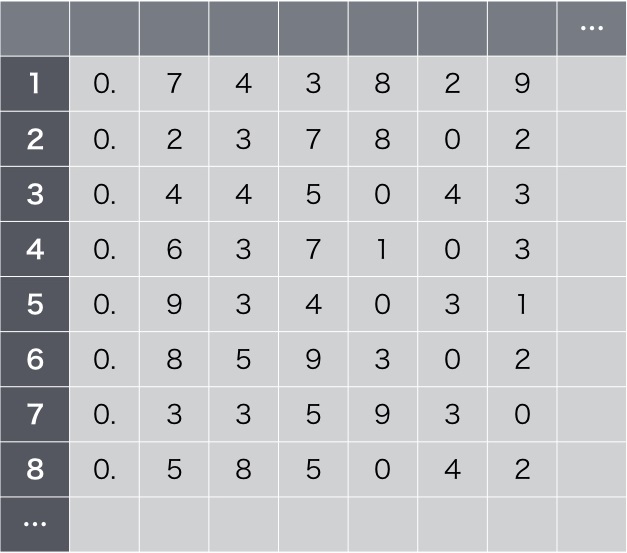
0と1の間の実数を並べた表。右側と下側は無限に続くので、すべての実数が並べられていることになる。
実数に対する背番号が左に並んでいるが、これは自然数。従って0と1の間の自然数と実数の個数は同じになる。
この表のどこに矛盾があるのでしょうか。ここで、斜めの対角線の部分の数字に1を加えます。すると、斜めに0.846243…という新しい実数が出てきます。
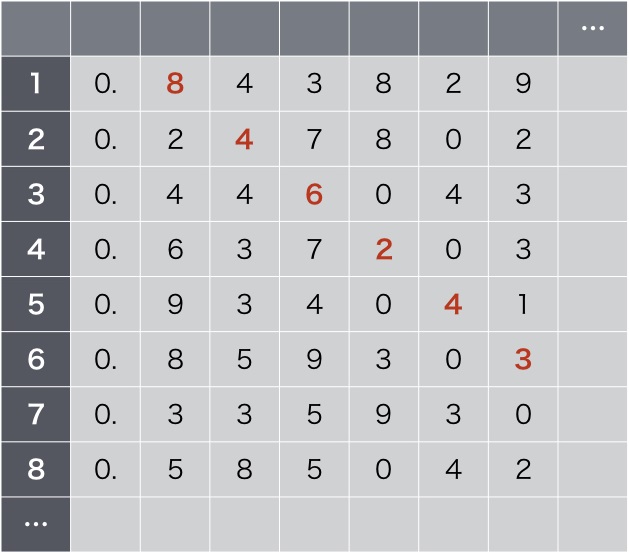
斜めに1を加えて、新しい実数を作る。
この実数は、この表のどこかに書いてなければおかしいということになります。なぜなら、この表には0と1の間の実数が無限に書いてあるはずです。
しかし、この0.846243…という実数は、どこにも存在できません。
まず、背番号1の実数ではありません。なぜなら、小数点1桁目に1を加えたのだから、同じ数になることがないからです。背番号2の実数でもありません。これも、小数点2桁目に1を加えたのだから、同じ数になることがないからです。背番号3の実数でも同じです。
このように、0.846243…という実数は、表の中のどの実数とも違うことになります。これは「すべての実数が列挙されている」ということと矛盾をすることになります。
これで、「自然数(表における背番号)と実数の個数は同じ」という前提条件が間違っていて、「自然数と実数の個数は同じではない」ということが証明できます。チューリングは、この論法をチューリングマシンに適用して、数学の不完全性を証明しようとしました。
チューリングとカントールの論法
チューリングもカントールの論法に則り、どんな計算も可能なチューリングマシンは存在しえないこと(=数学の不完全性)が証明されました。しかしチューリングは、この論法をただ模倣したのではなく、彼独自の"発想"を付け加えます。これは、コンピューターの発展史にとって極めて重要なことでした。
この発想こそが後に「フォン・ノイマン型コンピューター」の特徴へと繋がります。今、私たちが使っているコンピューター、もちろんスマートフォンも、フォン・ノイマン型です。チューリングがこの発想にたどりつかず、米国の科学者フォン・ノイマンがその意味に気づかなかったとしたら、今あるコンピューターやスマートフォンの開発は数十年は遅れていたといっても過言ではないでしょう。
そこで、チューリングの証明を紐解く前に、この"発想"と現在のコンピューターとの関わりについて述べていきます。これはチューリングの証明方法を理解する上でも、重要な手がかりとなります。
チューリングの大胆な発想とフォン・ノイマンの発見
チューリングがチューリングマシンの論文を発表した後、米国ペンシルバニア大学では、世界初の電子計算機「ENIAC」の開発が始まりました。しかし、ENIACは、現在私たちが知っているコンピューターとはずいぶん姿が違っていて、実態は「ケーブル接続された電卓」に近いものでした。
例えば、(A+B)×Cという計算をさせたいとき、足し算専用電卓と、かけ算専用電卓をケーブルで接続します。足し算専用電卓に、「A」と「B」という数値を入力すると、その結果がケーブルでかけ算専用電卓に送られます。
かけ算専用電卓は、送られてきた数と「C」という数を掛け算し、結果を出力。ENIACはそういう構造でした。これは、現在のプログラムに相当するとしたらいわゆるケーブル接続であり、異なる計算をさせたいときはケーブルをすべて抜いて、どのように配線したら目的の計算ができるかを考え、大量のケーブルを挿してやる必要がありました。
ENIACの開発プロジェクトに参加した数学者フォン・ノイマンは、ケーブル方式が大いに不満でした。なぜなら、計算の設定(プログラミング)に膨大な時間がかかるだけでなく、「ケーブル接続された電卓」方式のため、複雑な計算はできないからです。
フォン・ノイマンは、チューリングのチューリングマシンの論文を読み、チューリングマシンでは、プログラムをデータと同じように扱っていたことに衝撃を受けます。フォン・ノイマンは、この発想を応用すれば、「ケーブル接続された巨大電卓」を「電子頭脳」に進化させることができると気がつきます。

By United States Army [Public domain], via Wikimedia Commons
ENIACのメイン制御パネルを2人のプログラマが操作しているところ
プログラムとデータを同列で扱うフォン・ノイマン型コンピューター
ENIACでも、データは真空管を使ったメモリーに保存します。しかしプログラムは、リアルな導線の接続方法で表現されます。フォン・ノイマンは、プログラムも数値に置き換えて、メモリーに置いてしまえばいいと考えました。メモリーの中のどのプログラムを実行するのかは、インディケーターを設定して「今、実行するのは○番地の命令」と示すようにすればよく、このインディケーターもデータになります。ということは、数値を自由に変えることができます。
「もし、変数Aが0より大きければ○番地のプログラムを実行。もし変数Aが0未満であれば△番地のプログラムを実行」という条件分岐や、「○番地のプログラムを実行したら、もう一度△番地のプログラムに戻る」というループができるようになります。それまでの導線を接続するプログラムと比べて、はるかに多彩で複雑な計算ができるようになったのです。
チューリングの「プログラムとデータを同列に扱う」という発想は、彼の論文の「停止判定マシン」のところで登場します。これをフォン・ノイマンが、実用のコンピューターに応用をしました。チューリングのコンピューター発展史に対する功績は、「チューリングマシンの考案」よりも「停止判定マシンの中で、フォン・ノイマン型コンピューターの原理を考案」したことの方がはるかに大きいといえます。
チューリングの証明した「代数学の不完全さ」~判定停止マシン~
果たしてチューリングは、「代数学の不完全さ」をどのように証明したのでしょうか。
チューリングマシンは、紙テープに書かれたデータを読み込んで、計算をする理論上の機械です。原理的に、適切なプログラムを書いてやりさえすれば、どのような計算もできるはずでした。しかし、その万能であるはずのチューリングマシンにも計算できない実例を見つければ、「代数学は完全ではない、不完全である」ということが証明できることになります。
そこで、さらに編み出されたものが「停止判定マシン」という理論でした。
チューリングマシンのプログラム(紙テープを読み込み、ヘッドを左に移動など)は、数値に置き換えることができます。つまり、紙テープに書いておくことができます(この点がフォン・ノイマンを驚愕させました)。
チューリングは、このプログラムを読み込んで、チューリングマシンが無限ループに入っていつまでも計算し続けるのか、計算を終了して停止出来るかを判定する別のチューリングマシン「停止判定マシン」を想定しました。
ここまで、チューリングの論理に穴はありませんでした。しかし、この停止判定マシンがさまざまな矛盾を引き起こし、前提である「停止判定マシンが作れる」が、否定されることになります。否定されれば、万能であるはずのチューリングマシンにもできないことがあるということが証明されることになり、「数学にもできない計算がある」ということが証明されます。
チューリングは、さまざまな停止判定マシンのプログラムを、停止判定マシンに評価させるという一覧表を作りました。そして、前編で紹介したカントールのロジックを使って、矛盾を指摘します。
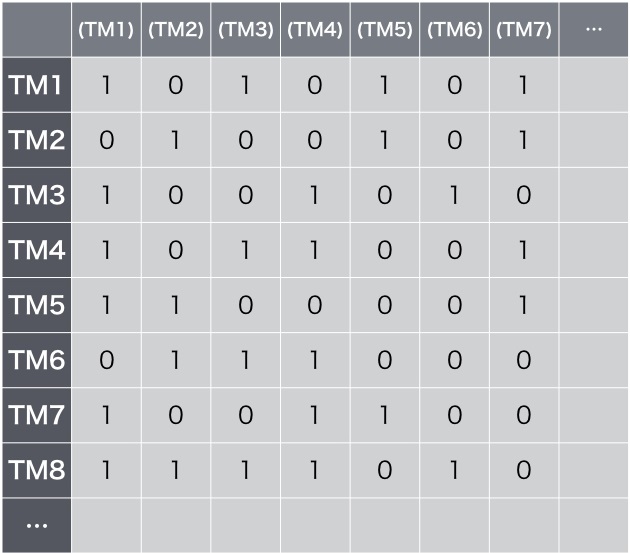
チューリングは、カントールの表とよく似た表を作った。
ここにはすべての停止判定マシンの判定結果が列挙されている。
右側と下側は無限に続く。
表のいちばん左上は、TM1という停止判定マシンが、(TM1)、(TM2)…と、それぞれの停止判定マシンが停止するかどうかを判定した結果です。停止の場合は1、無限ループに入って停止しない場合は0が出力されます。
2行目は、TM2という別の停止判定マシンが(TM1)、(TM2)…と、それぞれの停止判定マシンが停止するかどうかを判定した結果です。
ここで対角線部分を反転させ、0010111…という新しい結果を作り出します。この0010111…は、この表の中にあるでしょうか。この表には、ありとあらゆる停止判定マシンの結果が列挙されているのだから、どこかに存在しなければなりません。しかし、存在していません。
1行目の結果は、1桁目が1が0に反転されているから、絶対に違います。2行目の結果は、2桁目の1が0に反転されているから、これも絶対に違います。3桁目の結果は…と、どこまで数字を変えていっても、0010111…は存在しません。
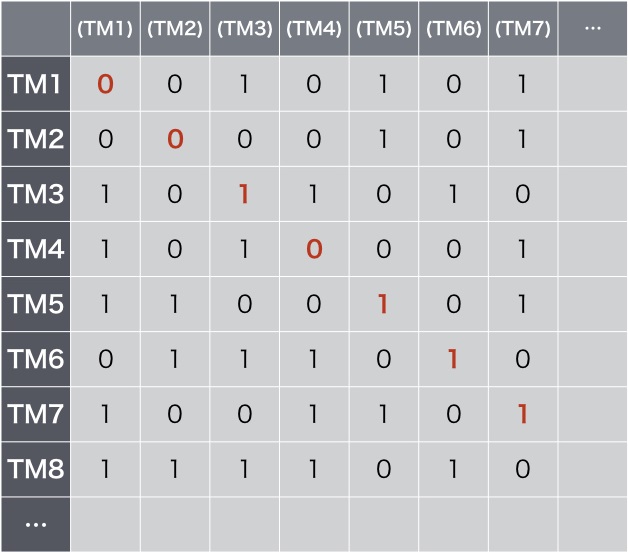
斜めを反転、新しい結果(反転)を作り出す
あらゆる結果が列挙されている表であるはずが、存在できない結果があるという矛盾を起こしています。これは、前提条件に誤りがあったからです。誤りというのは「停止判定マシンが作れる」という前提でした。結論は「作れない停止判定マシンがある」ということだ。つまり、どんな計算でもできるはずのチューリングマシンにも、「停止判定」というできない計算が存在したということになります。
ハッカー的手法だったチューリングの論文
チューリングは、計算の不完全さも証明し、この研究を「計算の可能性と、その決定問題への応用」という論文にまとめます。「計算には不可能なものがある」ということが「計算の可能性」であり、「可能か不可能かをどうやって決めたらいいのか」ということが「その決定問題」です。
チューリングは、この論文を発表したことで、数学者として認められ、米国プリンストン研究所への留学が決まり、そこでアルバート・アインシュタインやフォン・ノイマンと出会うことになります。また、イギリス情報部もこの論文に注目をし、帰国したチューリングをヒトラー暗号の解読の仕事に抜擢しました。
チューリングの偉大さは、従来とはまったく違ったアプローチで、数学の根源的な問題に挑戦したことにあります。ここまでの説明を難しいと感じられている方も多いと思います。ただもし、この偉業を伝統的な数学者が伝統的な手法で行っていたとしたら、それは数学者でしか理解のできない内容になってしまうでしょう。
チューリングの手法は、多分にハッカー的な手法で、門外漢にも難しいとは言えなんとか理解できる範囲に収まっているのです。
最後まで「自己流」を貫き通したアラン・チューリングの生涯
暗号解読を終えたチューリングは、エニグマ暗号の解読法を解説した「プロフ・ブック」と呼ばれる論文の執筆を依頼されます。読むのは、暗号解読の専門家であるはずなのに、チューリングは数式を使わず、実例を多く使い、普通の人が読んでも理解できるようなものに仕上げることに注力しました。
しかし、チューリングは、どのような説明にすれば、普通の人にもわかりやすくなるのかよくわからず、試行錯誤をしながらの執筆だったとされます。それを補佐したのが、チューリングの生涯の中で、たった一人だけ女性だった恋人のジョーン・クラークでした。チューリングは執筆中、ジョーンを隣に座らせ、たびたび「これでわかりやすくなったかな?」とアドバイスを求めていたといいます。ジョーンは、チューリングの肩に頬を寄せて、執筆中の論文を覗き込み、的確なアドバイスを加えていたとされています。
しかし、この美しく切ない恋は実ることはなく、そればかりか、チューリングは犯罪だとされていた同性愛を公表してしまうことになり、逮捕されることになります。名誉も剥奪され、逮捕後は薬物治療を受けていましたが、42歳の若さで自死を選ぶことになりました。
その後、1970年に「ウルトラシークレット」という書籍が、戦時中当時の軍事機密を公表するまで、チューリングは世間に広く知れ渡ることはありませんでした。
そして2009年に、英国政府は、名誉はく奪したことを正式に謝罪し、2013年には正式に名誉回復されています。しかし、彼の功績が認められる頃には、彼はもう亡き人でした。


