TOUCH THE SECURITY Powered by Security Service G

あなたは、自宅玄関の合鍵をどこに隠しているでしょうか。玄関マットの下や植木鉢の下というのが定番ですが、私は郵便受けの中にテープで貼り付けています。郵便受けはダイアル錠になっているので、番号を知らなければ開けることができません。つまり、二重の鍵で保管していることになります。
ネットワークを使って、重要な通信をする時、例えば業務関係のメール、ECサイトでのカード情報を始めとする個人情報をやりとりする時は、暗号化をしなければなりません。暗号化というのは、宝箱にデータを入れて、鍵をかけて渡すということと同じです。
しかし、鍵はどうやって受け渡ししたらいいでしょうか。送信者と受信者の双方が同じ鍵をに渡してあげなければ、受信者は宝箱を開けることができません。しかし、その鍵のやりとりの最中に鍵が盗まれてしまったら、悪人に簡単に宝箱を開けられてしまいます。
だったら、鍵も箱にしまって鍵をかけて渡せばいい。でも、その箱の鍵はどうやって渡す?それも箱にしまって…。じゃあ、その箱の鍵は?となって、終わりがありません。双方が同じ鍵を使う共通鍵暗号方式では、「安全な鍵の受け渡し」が常に問題になるのです。
目次
1.閉める鍵と開ける鍵を別々に ~一方向関数と公開鍵暗号方式~
1960年代に、この問題を解決する方法を思いついたのが、イギリスの政府通信本部の暗号学者ジェームズ・エリスでした。政府通信本部は、第2次世界大戦中、アラン・チューリングなどが在籍し、ヒトラーの暗号「エニグマ」の解読に成功したブレッチリー・パークを継承した機関です。現在でも、電子的な暗号解読、情報を分析を行うシギント業務を担当しています。
エリスの発想は単純でした。「閉める鍵と開ける鍵を別々にすれば、鍵をやりとりしなくて済む」というものでした。送る方は、最初から閉める鍵を持っておき、受け取る方は、最初から開ける鍵を持っておけば、鍵をやり取りする必要はありません。
しかし、ふたつの鍵がまったく無関係では、閉める鍵で閉めたものを、開ける鍵で開けることができません。なんらかの関係はあるけど、別の鍵。そんな都合のいい鍵を見つける必要がありました。
イギリス政府通信本部のエリスの後輩であるクリフォード・コックスは、そのような都合のいい鍵のペアを作るには、一方向関数を使えばいいと思いつきました。しかし、そんな都合のいい関数を見つけることができません。同じ頃、米国のホイットフィールド・ディフィーとマーティン・ヘルマンが、実用的な一方向関数を見つけて、公開鍵暗号の具体的な理論を構築します。
2.組み合わせるのは楽ちん、バラすのは大変。一方向関数
果たして一方向関数とは何か。これをテトリスに例えてみよう。
テトリスのブロックを組み合わせて、四角を作るのはさほど難しくはありません。試行錯誤で組み合わせてみればなんとかなりますし、テトリスの達人であれば、一瞬で四角を作れてしまうでしょう。
ところが、四角の状態から、「これをテトリスのブロックに分割しなさい」という問題はちょっと厄介です。【図1】では、ブロックの形に線が引いてあるので簡単ですが、この線が引かれてないとなると、試行錯誤をした上でかなり頭を使います。このように相互に変換できるのに、ある方向への変換は簡単なのに、逆方向の変換はたいへんというのが一方向関数です。

【図1】積を求めるのは楽でも、逆の商を求める計算は手間がかかる。このような一方向関数の発見が公開鍵暗号の基礎になっている。
そこで、コックスが見つけたのは、素数の積と素因数分解でした。例えば、143という数があります。これを素因数分解するというのはけっこう手間がかかります。中学校で習った「まず2で割り切れるかどうかを確かめ、次に3で割り切れるかどうかを確かめ…」という、小さい素数から順番に割ってみていくしか方法がないからです。
例に挙げた143は11×13と素因数分解することができます。しかし、逆方向である素数の積「11×13」を計算することはさほど難しくありません。このような一方向関数を使うというのが公開鍵のポイントです。
3.公開鍵で閉めて、秘密鍵で開ける
このような一方向関数を使って、公開鍵と秘密鍵の2つの鍵のペアを作るのが公開鍵暗号の基本になります。先ほどの例で言えば、公開鍵は143、秘密鍵は(11、13)ということになります。
秘密鍵から公開鍵を作るのは簡単ですが、公開鍵から秘密鍵を推測するには膨大な計算時間が必要になります(実際の公開鍵暗号では、膨大な桁数の素数を利用します)。公開鍵から秘密鍵を推測するのは、時間とCPUパワーをかければ不可能ではありませんが、一般的な情報通信の場合、推測の演算に数十年、数百年かかってしまうのであれば、その頃には情報を秘匿する意味がなくなっています。
公開鍵は、誰でも自由に利用できるように公開されていて、閉める専用の鍵です。秘密鍵は、受信者だけがしっかりと管理をして、開ける専用の鍵です。情報を送りたい人は、受信者用の公開鍵を手に入れて、それで鍵を閉めて、受信者に送ります。受信者は自分だけが持っている秘密鍵で開ければいいというわけです。受信者が秘密鍵をしっかりと管理さえしていれば、情報は完璧に秘匿できます (【図2】)。
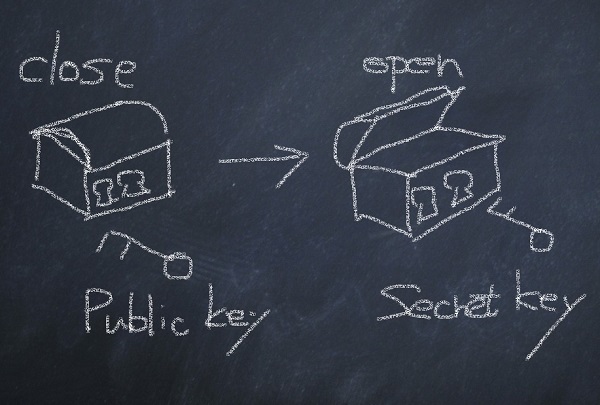
【図2】閉める鍵(公開鍵)と開ける鍵(秘密鍵)を別々にすることによって、鍵の受け渡し問題を解決した。
ところで、公開鍵と秘密鍵を使って、どのように暗号化(閉める)、復号化(開ける)を行っているのでしょうか。公開鍵暗号で最も有名なRSA暗号では、べき乗と剰余(割った余り)だけを使って、暗号化、復号化を行うという、実にシンプルで美しいアリゴリズムになっています。
RSA暗号のアルゴリズムの簡単な説明
数学が苦手だという方は読み飛ばしてください。
先ほどから、素数の積が公開鍵、素数のペアが秘密鍵と説明してきましたが、説明をわかりやすくするためにそうしたのであって、厳密には少し違います。RSA暗号では暗号化、復号化に次のようなアリゴリズムを使います。
- 暗号文=平文^E mod N
- 平文=暗号文^D mod N X mod Y:XをYで割った余り
暗号文を作る(E、N)のペアが公開鍵、平文に戻す(D、N)のペアが秘密鍵になります。両方の鍵に使われるNは素数の積です。計算が大変になるので、小さな素数、3と11を例に使いましょう。この場合、N=3*11=33となります。
次にDとEを求めますが、その前に計算に必要なFという数値をいったん求めます。
- F=LCM(p-1,q-1) LCM:最小公倍数
ここでは、(3-1,11-1)=(2,10)の最小公倍数ですから、F=10となります。ここからDとEを導いて、公開鍵、秘密鍵を求めることができます。
公開鍵のEは、GCD(E,F)=1となるようなEです(GCD:最大公約数)。つまり、Fとの最大公約数が1になるような数です。わかりやすく言えば、Fと「互いに素」であればいいわけで、そのような数はいくつもありますが、この場合は、GCD(E,10)=1なので、3にしておきましょう。E=3となり、公開鍵は(3、33)となります。
次に、秘密鍵のDは、(D*E) mod F=1となるようなDです。つまり、DとEの積をFで割った数が余り1となるような数です。(D*3) mod 10=1になるDを求めると、D=7になります。これで秘密鍵は(7、33)となりました。
公開鍵の情報から秘密鍵を類推するには、Nを素因数分解し、F=LCM(p-1,q-1)を計算してFを求め、さらに(D*7) mod F=1となるようなDを求めなければなりません。小さい数を使っても計算はけっこう大変なのですから、これで桁数が大きければ、膨大な計算量になることは容易に想像できると思います。
では、実際に17という数を暗号化してみましょう。
- 暗号文=17^3 mod 33=4913 mod 33=29
この29という暗号文を受け取った受信者は、自分の秘密鍵を使って、
- 平文=29^7 mod 33=17249876309 mod 33=17
と、平文17に戻りました。
数学が得意な方は、なぜこうなるのかを考えてみると楽しいと思います。また、プログラミングのスキルがある方は、より大きな素数を使って、コーディングしてみると楽しいでしょう。
4.秘密鍵で閉めて、公開鍵で開けると電子署名になる
この公開鍵と秘密鍵を逆に利用すると、あなたが本当にあなたであることを証明する電子署名になります。
まず、あなたは、自分の名前を、自分だけが持っている秘密鍵で暗号化をします。これを受信者に送ります。受信者は、どこからでも手に入れられるあなたの公開鍵を使って、復号化をします。すると、あなたの名前が現れます(【図3】)。このようなことができるのは、(管理がきちんとしているのであれば)秘密鍵を持っているあなただけです。確かにあなたからの文書であるという証明になります。
あなたの公開鍵は、誰でも手に入れることができます。ですから、誰でもあなたの電子署名を開いてしまうことができます。しかし、ただのサインですから、それで問題ありません。
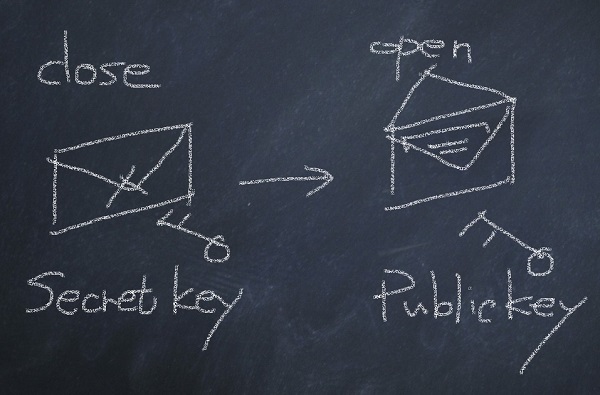
【図3】公開鍵と秘密鍵を逆に使うと、本人が本人である証明ができる電子署名になる。
5.共通鍵を公開鍵で閉めて送ると、暗号通信ができる
公開鍵暗号は、「鍵のやりとりをしないで済む」という賢い方法です。しかし、欠点もあります。それは、暗号化、復号化に計算時間がかかるということです。電子メールのようなものでは、あまり大きな問題にはなりません。送信するときに暗号化をし、受信をするときに復号化をしても、体感するほど遅くなることはありません。しかし、ウェブとの通信では、何度となくデータがやり取りされるので、そのたびに暗号化と復号化をしていたら、さすがに遅く感じることになるでしょう。
しかし、クレジットカード情報や個人情報をやり取りするECサイトの通信では、暗号化は必須です。そこで、SSL(Secure Sockets Layer)では、共通鍵暗号と公開鍵暗号を組み合わせて使います。
共通鍵暗号は、シンプルなので、暗号化、復号化に時間がかかりません。しかし、鍵のやりとりに危険が付きまといます。そこで、SSLでは、共通鍵を公開鍵で暗号化して安全に渡すのです。ここがポイントです。
あなたがECサイトに接続すると、ECサイトは自分の公開鍵をあなたに送ります。あなたは共通鍵を作って、それをECサイトの公開鍵で暗号化します。これをECサイト側に送ると、ECサイトは自分の秘密鍵で復号化します。中からは、あなたが作った共通鍵が現れてきます。つまり、やりとりに危険が伴う共通鍵を、公開鍵暗号の仕組みを使って安全に送り、以降の通信は共通鍵を使って暗号化をするという仕組みです(【図4】)。
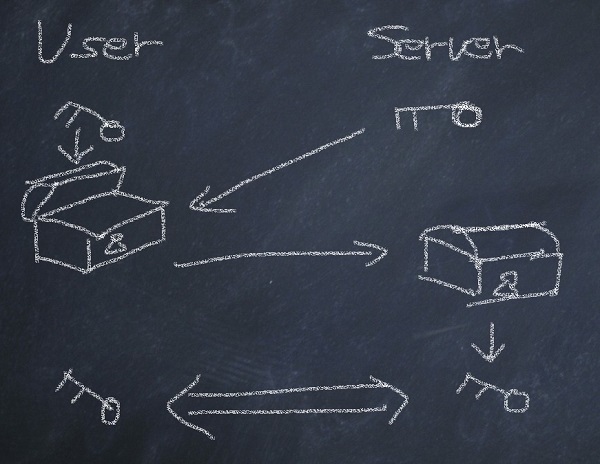
【図3】公開鍵と秘密鍵を逆に使うと、本人が本人である証明ができる電子署名になる。
もちろん、このような操作は、ブラウザーが自動的に行ってくれるので、あなたはセキュアなSSL通信が確立しているかどうかを確認するだけでかまいません(URLがhttpsで始まっていることを確認すればいいのでした)。
公開鍵暗号というと、特別な人だけが使うもののように思っている方もいるかもしれませんが、実は私たちのほとんどが毎日使っているものなのです。


